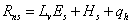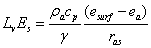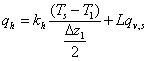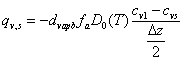Surface energy balance approach

Soil evaporation, Snow and Radiation processes > Evaporation from the soil surface

Surface energy balance approach

The physically based approach, for calculating soil evaporation, originates from the idea of solving an energy balance equation for the soil surface. According to the law of conservation of energy the net radiation at the soil surface, R_ns, is assumed to be equal to the sum of latent heat flux, L_vE_s, sensible heat flux, H_s and heat flux to the soil, q_h:

(4.2)

The three different heat fluxes are estimated by an iterative procedure where the soil surface temperature, T_s, is varied according to a given scheme until eq. (4.2) is balanced:

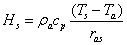(4.3)

(4.4)

(4.5)

where r_as is the aerodynamic resistance calculated as a function of wind and temperature gradients (Eq. (4.12) - (4.24)), k_h is the thermal conductivity of the top soil layer, e_surf is the vapour pressure at the soil surface (eq. (4.7)) and e_a is the actual vapour pressure in the air. The density, ρ_a, heat capacity of air, c_p, the latent heat of vaporisation, L_v, as well as the psychrometer constant, γ, are all considered as physical constants. The vapour flow, q_v,s, (following eq. 2.12) from the soil surface to the central point of the uppermost compartment is given by:

(4.6)

where d_vapb is the tortuosity given as an empirical parameter, D₀ is the diffusion coefficient for a given temperature, f_ais the fraction of air filled pores (θ_s-θ) and c_vsand c_v1 are the concentrations of water vapour at the soil surface and at the middle of the uppermost compartment respectively.

A plastic sheet can optionally be included in the simulation (see switch Surface cover). This sheet prevents soil evaporation from the fraction, i_scovevap.

Vapour pressure at the soil surface

Resistance approach for soil heat flow

Aerodynamic resistance with stability correction below vegetation canopy