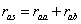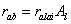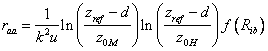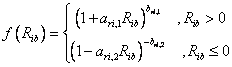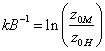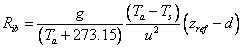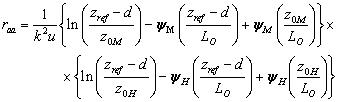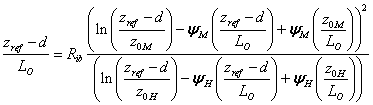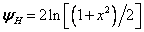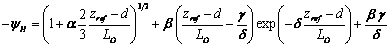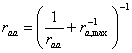Aerodynamic resistance with stability correction below vegetation canopy

The aerodynamic resistance above the soil surface, r_as, is calculated as a sum of two components – a function of wind speed and temperature gradients, r_aa, which is corrected for atmospheric stability, and an additional resistance representing the influence of the crop cover, r_ab (see viewing function Aerodynamic Resistance, r_as):

                                                              (4.12)

The influence of the crop canopy on the aerodynamic resistance above the soil surface is made proportional to the leaf area index, A_l:

                                                                (4.13)

where r_alai is an empirical parameter (see viewing function Aerodynamic Resistance below canopy, r_ab).

The influence of atmospheric stability on the aerodynamic resistance, r_aa, can be calculated either as (I) an analytical function of the Richardson number or (II) as a function of the Monin-Obukhov stability parameter (see switch Stability Correction). Method (I) is preferred from a computational point of view, since (II) involves an iterative solution of the relation between the Richardson number and the Monin-Obukhov stability parameter (Eq.(4.19)). However, only method (II) allows for a consistent treatment of variations in the roughness lengths for momentum and heat.

(I) The aerodynamic resistance at neutral conditions is multiplied by an analytical stability function:

                         (4.14)

 

 

where u is the wind speed at the reference height, z_ref, d is the zero level displacement height (c.f. Potential Transpiration in Plant Water Processes), R_ib is the bulk Richardson number (eq.(4.17)), k is the von Karmans constant and z_0M and z_0H are the surface roughness lengths for momentum and heat respectively. If z_0M is exchanged to z_0M,snow the equation can be used for snow surfaces. f(R_ib) is a function that governs the influence of atmospheric stability:

                                (4.15)

 

 

where a_ri,1, b_ri,1, a_ri,2 and b_ri,2 are empirical parameters.

The surface roughness length of momentum, z_0M, can either be given as a specific parameter for different sub-surfaces (i.e. bare soil, snow and canopies) or as a function of canopy height (c.f. “Potential transpiration” in Plant Water Processes). The surface roughness length of heat, z_0H, is then derived from:

                                                         (4.16)

 

where kB^-1 is a parameter with a default value 0 (implies z_0H=z_0M). The parameter is the product of a von Karmans constant, k, and a parameter, B, but since it is often found in the literature as kB^-1 we have kept it as such in the model.

The bulk Richardson's number is calculated as:

                              (4.17)

 

 

(II) The aerodynamic resistance as a function of the Monin-Obukhov stability parameter, (adopted from Beljaars and Holtslag,1991):

           (4.18)

 

 

where L_O is the Obukhov length and Ψ_Μ and Ψ_Η are empirical stability functions for momentum and heat respectively (unfortunately the nomenclature coincides with that for latent heat of vaporisation and water tension). The relation between the Obukhov length and the Richardson number is specified by the following equation:

    (4.19)

 

 

which is solved by an iterative procedure following Beljars and Holtslag (1991). The empirical stability functions is calculated for unstable conditions ((z_ref-d)/L_O<0) by:

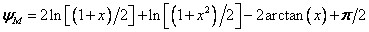    (4.20)

 

and

                                                 (4.21)

 

where

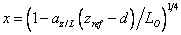                                          (4.22)

where the non-optional parameter value a_z/L=19 was taken from Högström (1996).

For stable conditions ((z_ref-d)/L_O>0) the empirical stability function is instead calculated as:

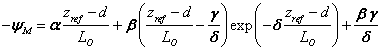  (4.23)

 

(4.24)

 

following Bejaars and Holtslag (1991), with the non-optional parameter values α=1, β=0.667, γ=5 and δ=0.35.

Furthermore, an upper limit of the aerodynamic resistance in extreme stable conditions is set by the “windless exchange” coefficient, r_a,soil,max^-1, adopted from Jordan (1991). It is applied in both (I) and (II):

                                                    (4.25)