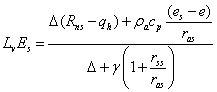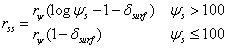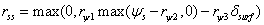Empirical approach for soil evaporation

The empirical approach for soil evaporation is based on the Penman combination equation[1] as suggested by Monteith (1965). It uses the available energy at the soil surface, R_ns-q_h, to calculate latent heat flux from the soil surface, L_vE_s, from which the soil surface evaporation, E_s, can be derived:

                                   (4.26)

 

 

where R_ns is the net radiation at the soil surface, q_h is the soil surface heat flux from the previous time step, r_as is the aerodynamic resistance, r_ss is the surface resistance at the soil surface, e_s is the vapour pressure at saturation in the air, e_a is the actual vapour pressure in the air, and ∆ is the slope of saturated vapour pressure versus temperature curve. The density, ρ_a, and heat capacity, c_p, of air, the latent heat of vaporisation, L_v, as well as the psychrometer constant, γ, are all considered as physical constants.

The aerodynamic resistance between the soil surface and the reference height, r_as, is calculated in the same way as in the physically based approach using Eq. (4.12)- (4.15).

The surface resistance at the soil surface, r_ss, can be estimated by two different empirical functions accounting for moisture conditions at the soil surface and the water tension in the uppermost soil layer. The first approach (“PM-eq, Rs(1Par)”) is based on only one governing parameter:

                                 (4.27)

 

 

where r_ψ is an empirical coefficient and ψ_s is the water tension in the uppermost layer (see viewing function Surface Resistance, Penman eq. 1 par). The δ_surf is the mass balance at the soil surface in units mm of water (see eq. 4.9).

The second approach (“PM-eq, Rs(3Par)”) is based on three governing parameters:

                          (4.28)

 

where r_ψ1, r_ψ2 and r_ψ3 are empirical coefficients (see viewing function Surface Resistance, Penman eq. 3 par).

Optionally, (“K-function”) the soil evaporation can be estimated as the minimum value of the flow rate that could be supplied from the middle point of the uppermost soil layer and the potential rate according to Eq. (4.26)  taking r_ss=0.

The soil surface temperature will also be estimated (for all of the three approaches described above) if the switch

Surface cover

Value	Meaning
No	No surface cover
Plastic sheet	A plastic sheet covering parts of the soil and thus preventing soil evaporation.

Surface Temperature

is put to “f(PM-equation)”. This is done by first solving the heat balance equation for the sensible heat flow to the air as:

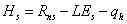                                                     (4.29)

where the soil surface heat flux, q_h, is taken from the preceding time steps. The soil surface temperature is finally given as:

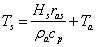                                                           (4.30)

Alternatively the soil surface temperature can be set equal to the air temperature except when snow covers the surface (option “Air temperature”).