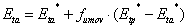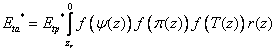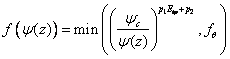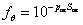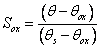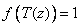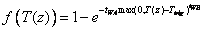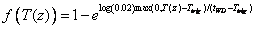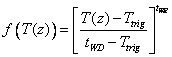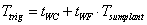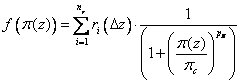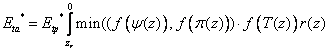Simple approach with response functions
Actual transpiration is calculated in two steps to account for possible compensatory uptake of water by roots in layers with no water stress if there are roots in other layers that are exposed to water stress. The actual transpiration is given as:
where fumov is the degree of compensation, Eta* is the uptake without any account for compensatory uptake and Etp* is the potential transpiration with eventual reduction due to interception evaporation. The compensatory uptake is distributed to the layers where no water stress occurs and in accordance with the relative fraction of the roots in these layers. In a first step the Eta* is calculated as the result of possible stresses at each depth and finally integrated as:
where nr is the layer with the deepest roots, r(z) is the relative root density distribution, zr is root depth and f(ψ(z)), f(π (z)) and f(T(z)) are response functions for soil water potential, soil osmotic potential and soil temperature. Root density may be expressed by root length per unit soil volume, or by any other pertinent measure of roots.
Reduction because of dry soil is supposed to act through the stomatal mechanism and xylary tissue resistance, which both have shown to be very sensitive to the demand rate. The water potential response function, f(ψ(z)), has been given a simple analytical form in the dry range:
where p1, p2 and ψc are parameters (Jansson, 1981). See viewing function Soil moisture response, simple response function. If the soil water potential is reaching the wilting point, ψwilt, the uptake is assigned to be zero from that horizon. An additional response function, fθ, correspond to the normal need of oxygen supply to fine roots and it has been given as:
where pox is an empirical parameter and Sox is a critical saturation range defined as:
when the soil moisture, θ, is above the critical soil moisture threshold, θox. The value of θox is calculated as the difference between the water content at saturation, θs, and the minimum air content, given as a parameter, θAmin. In case θ is less than the Sox, Sox is given a value of zero, which means that the response function is equal to unity, i.e. the maximum value.
Reduction because of low soil temperatures acts primarily through a lowered conductivity between root surface and xylem and is, thus, responding to temperature at each depth. There are different ways of estimating the soil temperature response, f(T(z)), which is determined by the switch Temperature response. By choosing “none”, there will be no reduction water uptake due to soil temperature:
The second option “Double-exponential”, is an analytical form of the soil temperature response, f(T(z)), which was proposed by Axelsson & Ågren (1976):
where tWA and tWB are parameters. Ttrig is the trigging temperature (see below). See viewing functions Soil temperature response, plant resistance and Soil temperature response, double-exponential.
A single-exponential function for the temperature response, f(T(z)), can also be used:
where tWD is a parameter. Ttrig is the trigging temperature (see below). See viewing functions Soil temperature response, plant resistance and Soil temperature response, single-exponential.
The forth alternative is to use a polynomial function for the temperature response, f(T(z)):
where tWD and tWE are parameters. Ttrig is the trigging temperature (see below). See viewing functions Soil temperature response, plant resistance and Soil temperature response, polynomial.
The trigging temperature, Ttrig, can either be a static parameter, tWC, or a function of air temperature (see switch Trigging Temperature). In the latter case the accumulated daily average air temperature above a threshold temperature determines the trigging temperature:
where tWC and tWF are parameters. Tsumplant is the accumulated sum of air temperatures above a critical temperature, tcrit (see Description of Plant).
The switch Salt Influence governs reduction of water uptake due to soil salinity. If the salt influence is set to be added to pressure head, the osmotic pressure, π(z), is added to the soil water potential, ψ(z), in eq (3.27). If this option is chosen the salinity response function, f(π (z)), in eq (3.26) will be put to unity. Alternatively the salt influence can be included as an independent response function by choosing “Add multiplicative response” or “Add minimum response”. This response function was proposed by van Genuchten et al(van Genuchten, 1983; van Genuchten & Hoffman, 1984; van Genuchten & Gupta, 1993) as:
where ri(∆z) is the relative root distribution, and πc and pπ are empirical parameter values. See viewing function Soil salinity response. The “Add Multiplicative response” option will multiply the response function for salinity, f(π (z)), with the other response functions for water and temperature as written in eq (3.26). On the other hand if the “Add minimum response” option is chosen, the smallest of the two response functions for soil moisture and salt, will instead be used in determining the water uptake, modifying eq (3.26)slightly into: