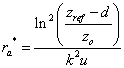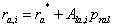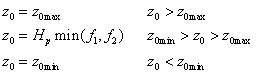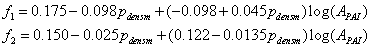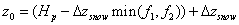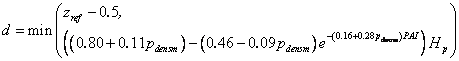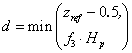Aerodynamic resistance
The aerodynamic resistance can be calculated with and without stability correction (see switch Aerodyn.Resistance). Without stability correction the aerodynamic resistance is calculated as:
where the wind speed, u, is given at the reference height, zref, k is von Karman’s constant, d is the displacement height and zo is the roughness length. See viewing functions Air and canopy resistances, Aerodynamic resistance affected by the parameters pdensm and paddind and Aerodynamic resistance affected by the parameter z0min.
If the aerodynamic resistance is calculated as a function of the Richardson’s number, eq. (3.15) is multiplied by the Richardson’s stability function as described in eq. (4.14)-(4-17). The stability correction can also be accounted for by calculating the aerodynamic resistance by the Monin-Obukhov stability function (eq. 4.18) instead of eq.(3.15). In both cases the roughness length used in the calculation of ra is the roughness length calculated for each plant (i.e. eq. (3.17)) and the parameter cH0,soil is exchanged to cH0, canopy.
If more than one canopy exist (see Description of Plant) additional contributions to the aerodynamic resistance will be estimated because of eventual shadowing of other canopies. The aerodynamic resistance for a specific canopy (i) is then calculated as:
where pral is a parameter and Ala,i is the leaf area index of all other canopies above the present canopy i. Roughness length and displacement height will be calculated based on either the height of the highest plant or for each plant individually (see switch MultiRoughness).
When simulating an explicit single big leaf plant the roughness length, zo, can either be given in a PG-file, read from a parameter table or estimated by functions following data presented by Shaw and Pereira (1982) (see Roughness). For multiple plants the roughness length is either calculated by the Shaw and Pereira function or is estimated by linear functions (see Roughnessfunc).
The Shaw and Pereira function calculate the roughness length as:
where z0max and z0min are parameters and where f1 and f2 are defined as:
and APAI is the plant area index, which is defined as the sum of leaf area index, Al, and the paddind which is a parameter together with Hp, pdensm and z0min. See viewing functions Roughness length, Shaw and Pereira, z0min, z0max and paddind and Roughness length, Shaw and Pereira, pdensm.
If snow is included in the simulation, the function for estimating roughness has to be adjusted in the following way:
where Δzsnow is the snow depth.
If roughness is determined by linear functions, f1 and f2 in eqs.(3.17) and (3.19) are replaced by the linear function calculated by eq.(3.3) and values found in the parameter table Roughness coefficients – multiple canopies. See viewing function Roughness length, linear function.
Also the displacement height, d, can be given in a PG file, read from a parameter table, or estimated by a function derived from suggestions presented by Shaw and Pereira (1982) (see switch Displacement). For multiple plants displacement is either calculated by the Shaw and Pereira function or is estimated by linear functions (eq.(3.3)) (see Roughnessfunc).
The Shaw and Pereira function calculates the displacement height as:
See viewing function Displacement height, Shaw and Pereira.
If snow is included in the simulation, the function for estimating displacement height has to be adjusted in the following way:
where Δzsnow is the snow depth.
If the displacement height is determined by linear functions, eq.(3.20) is modified into:
The linear function, f3, is calculated by eq.(3.3) and values found in the parameter table Displacement coefficients – multiple canopies. Eq.(3.21)is modified analogously. See viewing function Displacement height, linear function.