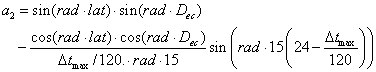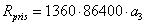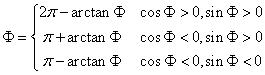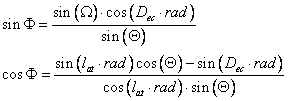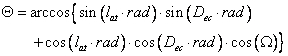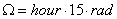Potential global radiation

Potential global radiation for daily mean values is given as a function of the solar constant, daylength, latitude and declination, D_ec:

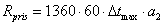                                              (4.90)

where 1360 is the solar constant (Wm^-2), 60 is the number of seconds per minute and a₂ is given by:

   (4.91)

 

 

where lat is latitude. The declination, D_ec, is given by Eq. (4.88) and the daylength, ∆t_max,  is given by Eq. (4.86). See viewing function Global radiation, potential.

Within day variation of potential global radiation is estimated as a function of hour of day, day of year and latitude following equation (4.92) -(4.101):

                                                 (4.92)

where 86400 is the number of seconds per day and a₃ is a geometric scaling function given by:

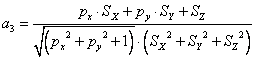                           (4.93)

 

 

where p_x and p_y are parameters defining the slope (m·m^-1) of the surface in the north-south and the west-east direction respectively (see “Meteorological Data”). This function can also optionally be used for correction of measured global radiation if the ground is sloping and the measured values are representing a horizontal plane (see switch SlopeCorrMeasuredGlobal):

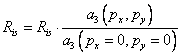                                          (4.94)

 

S_X, S_Y and S_Z are geometric functions related to the suns position at the sky given by:

                                                  (4.95)

where Φ is the azimuth angle and Λ is the elevation angle of the sun, which are given by

                         (4.96)

 

 

and

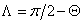                                                              (4.97)

respectively. The arctanΦ, sinΦ and cosΦ expressions in equation (4.96)  are given by:

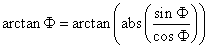                                     (4.98)

and

                     (4.99)

 

 

 

where Θ is the zenith angle and Ω is the hour angle of the sun defined by

                   (4.100)

 

 

and

                                                     (4.101)