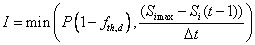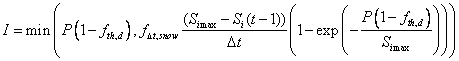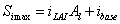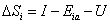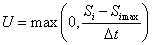Interception rate and interception storage

Interception rate can be calculated either by a simple threshold formulation or by an exponential function (see switch InterceptionModel). The threshold function gives the interception rate, I (mm day^-1), by the vegetation canopy.:

                           (3.51)

where P is precipitation, f_th,d is the fraction of the precipitation that directly reaches the soil surface without being affected by the vegetation, S_imax is the interception capacity, and S_i (t-1) is the interception storage remaining from the previous time step.

Alternatively, the interception rate, I, is calculated by an exponential function (Hedström & Pomeroy, 1998):

    (3.52)

where f_∆t,snow is a time step dependent “snow unloading” coefficient, representing the influence of snow falling of the canopy during and interception event. It is automatically set to unity if snow interception is not treated (see switch SnowInterception) and/or in case of liquid precipitation. For snow, f_∆t,snow is set to 0.7 for hourly time steps, and empirically corrected to obtain the same interception rates if other time steps are chosen.

The interception capacity (maximum storage) S_imax is a function of the leaf area index, A_l:

                                                                        (3.53)

where i_LAI and i_base are parameters. See viewing function Interception storage as a function of LAI.

The change in interception storage, ∆S_i, is calculated as the difference between the interception rate, I, and the actual interception evaporation, E_ia:

                                                         (3.54)

where U is the amount of snow falling off the canopy due to a changed interception capacity i.e. increased air temperature or snow melt in the canopy (cf. section Interception capacity with snow interception):

                                                (3.55)