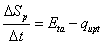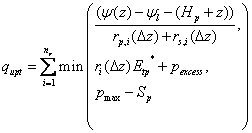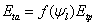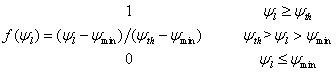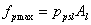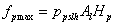Dynamic SPAC approach

In this approach the change of water storage in the plant, S_p, is calculated during the day. The change of plant water storage is defined as:

                                                          (3.43)

where q_upt is the water uptake rate calculated with an equation similar to the steady-state SPAC approach, eq. (3.37), but now without the direct connection to the potential demand:

                            (3.44)

where p_excess is a parameter determining the flow rate in excess of the potential demand from the atmosphere and f_pmax is a function that gives the maximal plant water storage as a function of LAI of the plant (see below). This parameter corresponds to the compensatory uptake rate from a single layer.

Note that in this approach the additional compensatory uptake mechanism that was included in the previous two more simplistic approaches are not applicable since the uptake rate is governed by a potential gradient and not a flux as in the previous approaches.

Since the SPAC-based formula is now used to calculate water uptake, the transpiration is instead given as:

                                                           (3.45)

where f(ψ_l) is a function that controls the opening of the stomata as a function of the leaf water potential, ψ_l:

           (3.46)

where ψ_min and ψ_th are parameters.

The leaf water potential is a linear function of the plant water storage given as:

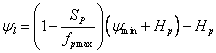                                   (3.47)

where S_p is the actual active plant water storage and f_pmax is a function that gives the maximal plant water storage as a function of LAI of the plant (if “f(LAI)” has been chosen):

                                                            (3.48)

where p_psl is a parameter. Alternatively the plant height may also be included in the function as (if “f(LAI, height)”has been chosen):

                                                                         (3.49)

where p_pslh is a parameter similar to p_psl.

Salt is treated analogous to the steady-state SPAC approach.